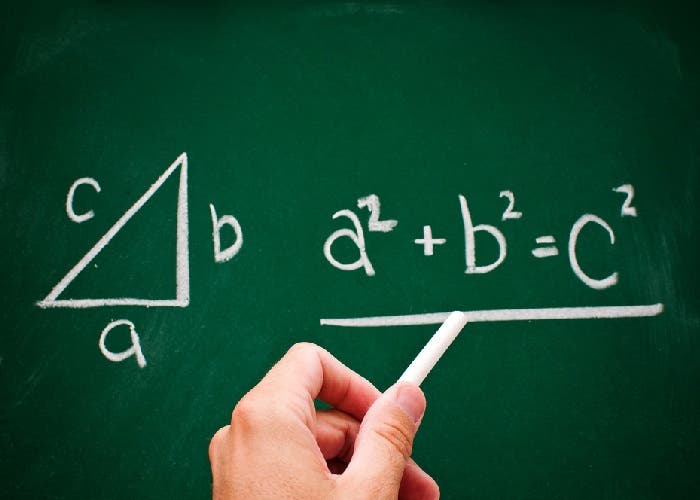
Hacia el año 530 a. C., Pitágoras aglutinó a su alrededor una hermandad entregada al estudio de las matemáticas. Pitágoras y sus discípulos creían en la divinidad de los números, a los que les atribuían pureza y la condición de inmutables ante los cambios materiales. Escudriñaban las relaciones numéricas entre las cosas y se les atribuye por ejemplo, el descubrimiento de que los sonidos producidos por una cuerda en vibración son armoniosos cuando la relación entre las longitudes de las cuerdas son números enteros (sin decimales). Aunque hay evidencias de que en la antigua Babilonia ya se conocía, fue probablemente Pitágoras quien demostró por primera vez el famoso teorema que expresa la relación entre los lados de un triángulo rectángulo.
Uno de los misterios matemáticos más antiguos de los que se tiene conocimiento, es la existencia de los números primos (números enteros sólo divisibles por sí mismos y por la unidad). No parece haber ninguna razón por la que tendría que haber números especiales, pero la verdad es que se cree que la cantidad de números primos es infinita. Estos números han fascinado a los matemáticos desde que fueron conocidos y el matemático griego Eratóstenes, desarrolló a través de su criba de Eratóstenes un método para determinar si un número es primo. Los números primos aparecen en diversas áreas de las matemáticas y son de gran utilidad en el desarrollo de la criptografía de clave pública.
El número π, es sin duda el más familiar de los números trascendentes. π es la relación entre la longitud de una circunferencia y su diámetro. El número π tiene una cantidad indeterminada de decimales (se han llegado a calcular más de un billón) y hasta hoy no se ha encontrado un patrón que describa la distribución de los mismos. Con el desarrollo de las matemáticas, a partir del siglo XVII se ha podido hallar expresiones ajenas a la circunferencia, donde aparece el número π. Ejemplo de ello es la fórmula integral de Cauchy integrada en el análisis de funciones con variable compleja.

El número de Euler (aproximadamente 2,71828) es otro ilustre número trascendente y aunque no tan conocido fuera del ámbito académico como el número π, es mucho más importante, ya que aparece en incontables disciplinas de las matemáticas, la física y la ingeniería. Es otro sorprendente ejemplo de número que se construye a partir de una sucesión (1+1/n) elevado a n, y aparece como por arte de magia en las más diversas expresiones matemáticas, como por ejemplo en cálculo de probabilidades, expresiones trigonométricas o en la teoría de cálculo integral con variable compleja.
Los números imaginarios constituyen sin duda la familia de números de carácter menos intuitivo ya que aparecen para dar solución a problemas en los que aparece la raíz cuadrada de -1. El concepto, aunque ya intuido por muchos matemáticos no fue introducido hasta el siglo XVI por el ingeniero italiano Rafael Bombelli. Posteriormente, Euler introdujo la notación i para representar la raíz cuadrada de -1. Como consecuencia de la introducción de los números imaginarios surgen los números complejos, constituidos por un binomio integrado por una parte real y una parte imaginaría (a+bi). Los números complejos han jugado un papel fundamental, por ejemplo en los cálculos de ingeniería eléctrica.
Sin embargo, la notación numérica no siempre ha sido como la usamos en la actualidad. No fue hasta comienzos del siglo XIII, cuando el comerciante italiano Fibonacci introdujo la numeración empleada por los indios, que junto al cero (llamado en árabe zephirum) se difundió con rapidez por toda Europa, por las evidentes ventajas que representaba frente a los números romanos.
Fibonacci, destacado matemático de la época, introdujo la sucesión de números: 1, 1, 2, 3, 5, 8, … (cada número es, a excepción de los dos primeros, suma de los dos anteriores). Esta serie aparece en muchos problemas matemáticos y sorprendentemente describe la distribución de las pipas de un girasol.

El concepto de cero parece hoy en día natural y evidente, pero en la antigüedad no se tenía el concepto de que “nada” pudiese ser un número. En Babilonia se dejaba un espacio donde correspondería un cero, lo que creaba confusión al distinguirlo de los espacios entre caracteres. Por otra parte, la falta del cero constituía el mayor inconveniente de los números romanos. Los chinos denotaban la complejidad de la idea de cero con el símbolo 零.
Si bien se sabe que el concepto ya era empleado por los mayas en el 650 a. C., parece que fueron los indios los que introdujeron el concepto de cero en Europa, oriente medio y China. El cero aparece en la actualidad en innumerables ecuaciones y principios científicos, como expresión de equilibrio de una igualdad matemática. Es el único que aparece en todos los conjuntos de números, a excepción de los números naturales.
La identidad de Euler que relaciona en una sola expresión los números más importantes de las matemáticas (0, 1, i, e, y π), ha sido considerada por los matemáticos como la expresión más bella por su simplicidad y elegancia:
![]()
Los matemáticos ni siquiera saben qué representa, pero saben que es correcta porque la han podido demostrar.
Los números son sin duda fascinantes. Cada día se descubren relaciones nuevas que resuelven importantes desafíos intelectuales y que expanden las fronteras de la ciencia. Otros están ahí, mostrando sorprendentes propiedades, como queriendo decirnos algo que no alcanzamos a descifrar. Se dice que la matemáticas simplemente se descubren y que el hombre no hace más que inventar la manera de describir lo que se ofrece ante sus ojos. Sólo hay que interpretarlo…
¿Te gustan las matemáticas? ¿Habías reflexionado alguna vez sobre la conexión de los números y los fenómenos de la naturaleza?

