Hoy en día estamos rodeados de objetos y construcciones “de diseño”, pero, ¿cuál es el elemento que poseen para ser tan atractivos o simplemente construibles? La respuesta la encontramos en las matemáticas, concretamente en el álgebra, la geometría y el cálculo infinitesimal.

El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades. El término “álgebra” viene de un vocablo árabe que significa reducción, cuyos orígenes se remontan a los antiguos babilonios, que habían desarrollado un avanzado sistema aritmético con el que resolvían cálculos en una forma algebraica. Con el uso de este sistema fueron capaces de aplicar las fórmulas y soluciones para calcular valores desconocidos. Permite la formulación general de leyes de aritmética , operar con números desconocidos y la formulación de relaciones funcionales.
La Geometría es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el espacio. Proviene del griego γεωμετρία, geo (tierra) y metría (medida). Ya en el antiguo Egipto el empleo de geometría estaba muy desarrollada para el cálculo de volúmenes y superficies en construcción.
El cálculo infinitesimal tiene amplias aplicaciones en la ciencia y la ingeniería y se usa para resolver problemas para los cuales el álgebra por sí sola es insuficiente. Este cálculo se construye con base en el álgebra, la trigonometría y la geometría analítica e incluye dos campos principales, cálculo diferencial y cálculo integral. Usualmente se le acredita a Leibniz y Newton la invención del cálculo, que , aunque desarrollaron sus teorías hacia diferentes aplicaciones empleaban ambos el teorema fundamental del cálculo.
A continuación expondremos las propiedades y funciones matemáticas mas empleadas en arte, diseño y construcción desde tiempos antiguos.
—-
Torre Eiffel (1889)
Esta estructura de hierro pudelado diseñada por Gustave Eiffel aplica el álgebra y el cálculo infinitesimal para desarrollar una ecuación adaptable al peso de la torre. Para hacernos una idea de cómo se aplica, antes se debe comprender qué es una ecuación exponencial.

Una ecuación exponencial es aquella ecuación en la que la variable a despejar se encuentra en el exponente, representada por una función exponencial, es decir, una gráfica que nos muestra su desarrollo. Las funciones son infinitas, pero acercándonos siempre a un límite conocido por asíntotas dándose el 0 (plano horizontal del suelo) y +∞ (el eje vertical de la torre). El matemático Weidman dedujo la base para la construcción de la torre. Un factor crucial para los cálculos que Eiffel tenía en mente pasaba por calibrar el efecto de las fuerzas ejercidas por el viento sobre determinados puntos estructurales de la Torre. Weidman encontró una solución exacta de la ecuación en forma de una función exponencial que se ajusta rigurosamente a la forma de la mitad superior de la torre.
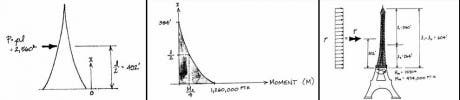
La clave para su solución deriva de dos ecuaciones exponenciales diferentes interconectadas: una para la mitad superior de la torre, y otra en la que interviene el factor de sobredimensionamiento de seguridad de la estructura en su base. Una construcción muy especial y emblemática sobre la que podéis ampliar información en este artículo de mi colega Jon Arregi. —-
Torre de Shújov (1920)
Construída en acero como una torre de transmisión para la red de radiodifusión rusa. Aplica una superficie englobada en el mundo de las cuádricas: el hiperbolóide de una hoja.
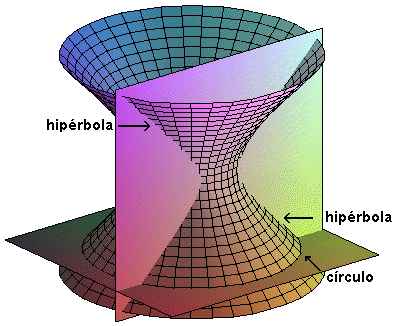
Esta superficie ha sido muy empleada en el mundo de la arquitectura para generar torres a partir de 1896, cuando el propio Shújov edificó una estructura paraboloide como mirador con una escalera de caracol en su interior.

Los beneficios de este tipo de estructuras son; su aerodinamismo: los empujes laterales y corrientes verticales del viento son disipadas por su forma hiperbólica, y su circunferencia de sección; y su equilibrio: al ser una figura plana de revolución de eje central, todos los puntos de una sección plana horizontal equidistan del centro, quedando así el eje y centro de carga en el centro.

—-
Olympiapark (1972)
La villa Olímpica, de 3 kilómetros cuadrados, fue construida en un terreno plano utilizado por el ejército hasta 1925 que se convirtió en parte del aeropuerto de Munich. Después de la Segunda Guerra Mundial en 1945, los escombros de la ciudad fueron trasladados aquí, formando la base del paisaje de colinas del parque olímpico. Empleado para las olimpiadas de Múnich 1972.

Construido por Günther Behmisch y Frei Otto & Partners, habiendo pasado a la historia por emplear complejas estructuras que interconectan mútliples paraboloides hiperbólicos, mi superficie favorita. Antes de entrar en el análisis del Olympiapark explicare una curiosidad de esta superficie cuádrica. El paraboloide hiperbólico también es conocido como ”silla de montar”, precisamente porque las monturas de los caballos poseen esta forma para adaptarse al lomo del mismo y suponer una comodidad para el jinete impidiendo que se deslice alante o atrás. Esta superficie tieme un punto muy característico denominado ”punto de ensilladura” que es a la vez máximo y mínimo de la superficie; es decir, que es el punto más alto de una parábola, y a su vez el más bajo de la otra.
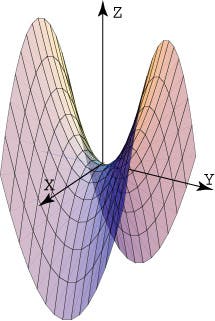
Las cubiertas de la villa olímpica de Múnich tienen aspecto de “tela estirada” y tensada por unas grúas, aunque en realidad son estructuras metálicas formando una malla revestidas por un tejido de poliéster recubierto de PVC (muy a la estética de los años 70). Este tipo de estructuras se dispersan a lo largo de toda la villa conformando parasoles de cara al verano, aunque también como resguardo de las lluvias características de la región, sin perder la luminosidad que nos ofrecen los rayos de sol que se filtran entre las nubes. Es toda una experiencia pasear bajo estas ”tiendas de campaña” un día lluvioso y observar el recorrido de las gotas de agua.

Hoy en día el conjunto conforma un parque público para la ciudad de Múnich, compuesto por: una pista de una pista de hielo, una piscina cubierta, una zona residencial, residencias de estudiantes y el Estadio Olímpico, que fue el hogar del FC Bayern München, hasta que se trasladó al futurista Allianz Arena en 2006.
—-
M. C. Escher (1898-1972)
Vamos con una de ilustración y artes gráficas. La obra de Escher experimenta con diversos métodos de representar (en dibujos de 2 ó 3 dimensiones) espacios paradójicos que desafían a los modos habituales de representación. A lo largo de su carrera realizó más de 400 litografías y grabados en madera, y también unos 2.000 dibujos y borradores. Un grupo importante está expuesto de forma permanente en el Museo Escher en La Haya, Holanda.

Las conocidas obras de este artista se basan fundamentalmente en tres componentes del mundo matemático: la geometría y perspectiva, la paradoja, y los fractales. Geométricamente su obra puede considerarse perfecta (hay que tener en cuenta que en aquella época no se empleaba la informática) ya que las seriaciones y los juegos de distancias y conexiones están medidas al milímetro. Sus famosas series de casas con escaleras o perspectivas imposibles fueron posibles gracias a la capacidad que tiene el cerebro humano para interpretar las 3 dimensiones y ser así engañado por trampantojos.

El complejo mundo de los fractales fue empleado para confeccionar las series dedicadas a la repetición infinitesimal. Un fractal es un objeto semigeométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas, es decir que podremos expandirlo infinitamente conservando su geometría base.

Las estructuras fractales son demasiado irregulares para ser descritas en términos geométricos tradicionales, poseen detalle a cualquier escala de observación, y son autosimilares, esto se explica con la curva de Kochs.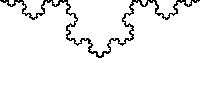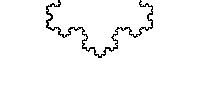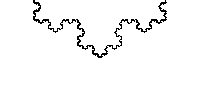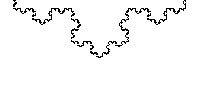
He aquí un ejemplo de composición en el campo de las artes gráficas basado en fractales.

—-
Echochrome (2008)
Este original y minimalista juego de Psp y Ps3 desarrollado por SCE Japan Studios junto con Game Yaruoze, nos propone unos retos en unos mundos que parecen creados por el propio Escher. Empleamos tres reglas básicas para conseguir llegar a diferentes puntos del espacio:
- Viaje en perspectiva: Por un cambio de perspectiva, puedes conectar diferentes caminos.
- Existencia de la perspectiva: Si tapas un vacío, podrá cruzarlo.
- Ausencia de perspectiva: Si tapas una obstrucción, podrá cruzarlo.
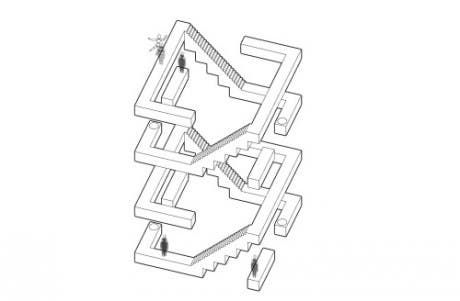
Esta ”perspectiva manipulable” por supuesto se desarolla en un entorno geométrico paralelo, es decir, no se emplea la perspectiva cónica, pudiendo jugar con la axonometría. Así conseguiremos una caballera, militar, ismoétrica… El mundo de la geometría se encuentra explotado al máximo en este aparentemente sencillo juego, ¿Veremos en un futuro la aplicación de los fractales de Escher en otra producción de SONY?


Información Bitacoras.com…
Valora en Bitacoras.com: Hoy en día estamos rodeados de objetos y construcciones “de diseño”, pero, ¿cuál es el elemento que poseen para ser tan atractivos o simplemente construibles? La respuesta la encontramos en las matemáticas, concretam……
Muy interesante la relación entre las matemáticas y la arquitectura
Gracias Jose! No nos libramos de ellas ni cuando acabemos la carrera! ¬¬’
[…] on xombit.com Me gusta:Me gustaBe the first to like […]
[…] perspectiva curieuse: La técnica se llama anamorfosis, y su origen se remonta al Renacimiento. Hans Holbein […]
[…] https://xombit.com/2011/06/la-importancia-de-las-matematicas-en-el-diseno-i […]
[…] Recuperado de: https://xombit.com/2011/06/la-importancia-de-las-matematicas-en-el-diseno-i […]
El diseño, un mundo apasionante. La Matemática, siendo un objeto ideal, con el diseño, alcanza su expresión real y su carácter de arte.